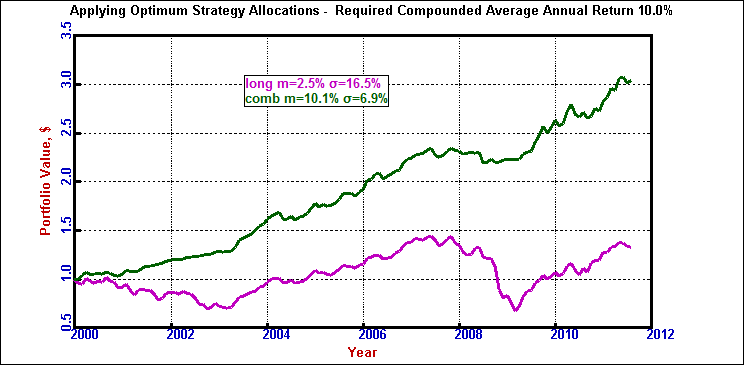
In the previous articles* on surviving market crashes we demonstrated how a market timing modification to Modern Portfolio Theory (MPT) provided asset allocation recommendations that resulted in the investor avoiding most of the losses during these market crashes. Not only that, but in the case of the dot-com bust, the model actually produced a significant positive return.
What is Modified Modern Portfolio Theory (MMPT)?
MMPT is the application of an optimized market timing strategy to MPT which not only produces superior returns but also does so at much lower risk than MPT. The reader is invited to read these articles* to become familiar with the basics of the approach which we call Modified Modern Portfolio Theory (MMPT).
In this article we will be considering the time of global instability arising from the debt crisis in the Eurozone in which we will show that the MMPT constructed portfolio would have significantly outperformed the classic MPT model portfolio.
Global Debt/Recession Fears
The movement of the market is heavily influenced by the uncertainty in the economic environment, and it is this uncertainty that is measured by the volatility index (VIX). Following a spike in volatility in March of 2011 resulting from the tsunami and nuclear plant meltdown in Japan, the volatility settled back down to stable levels below 20. But it began to rise again as both the domestic and Eurodebt crisis came to the forefront on the heels of sovereign debt downgrades heralded by some of the major ratings agencies.
It wasn’t until the end of July that the volatility began climbing to bearish levels (over 25). July 22nd was the last time the S&P 500 (SPX) hit a relative high of 1346 before the VIX took off, sending the S&P plunging 17% in a few short weeks. Following Standard & Poors downgrade of the US’s credit rating, the SPX hit a low of 1120 on August 8th as the VIX concommitantly hit a high of 48. After two months of extreme choppiness, the VIX hit another relative high on October 4th as the S&P put in an intraday low of 1075, representing an overall loss of 20% from its July high. (See charts below.)
Methodology
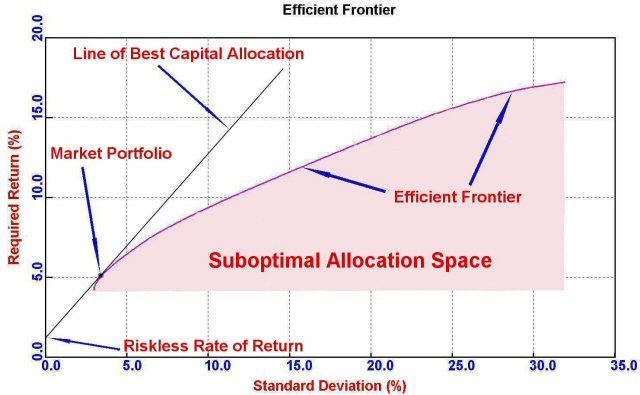
To compare how a modified portfolio would have done compared with a classic one, the reader should understand the underlying methodology. Both portfolios are made up of the same nine asset classes comprised of domestic and international stocks and bonds along with real estate (in the form of REITs). The model portfolios presented here are designed to return a 10% compounded annual return, the same that was used in the previous articles. The analysis rebalances the portfolios monthly as new total return asset class performance data is made available. The portfolio allocation tool used to conduct these studies for both the classic MPT model and the market timing MPT approach is the SMC Analyzer.
The allocations
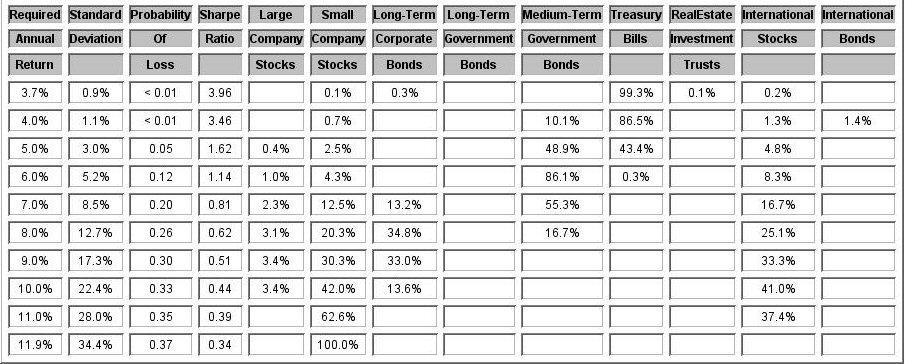
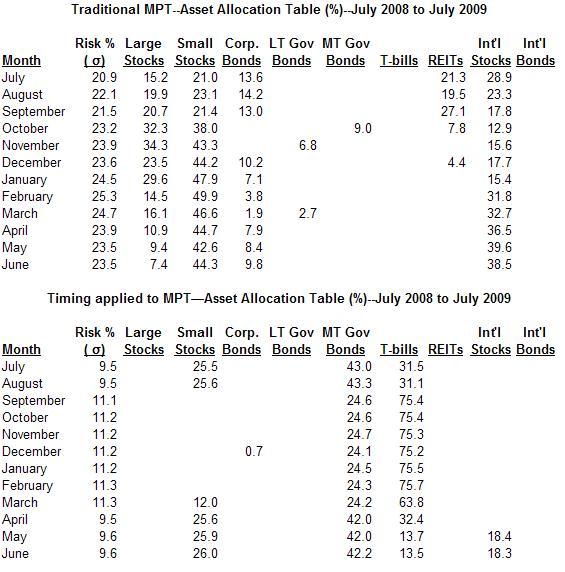
During this turbulent time period, an MPT portfolio with a 10% required annual compounded return would have been heavily invested in the stocks of large and small companies both domestic and international (see Table 1). But the MMPT equivalent model (see Table 2) was already light in the large and small stock asset class having benefited from the recent experience of the dot-com bubble and subprime mortgage collapse. Despite some optimism for the alternative international stock and real-estate investment trust asset classes the allocations there were comparatively light, instead heavily favoring medium-term government bonds and the safety of Treasury Bills (or an insured money market equivalent).
Table 1. Classic MPT Historical Allocations During the Subject Period for a Target 10% Compounded Annual Return
Table 2. MMPT Historical Allocations During the Subject Period for a Target 10% Compounded Annual Return
Comparing models
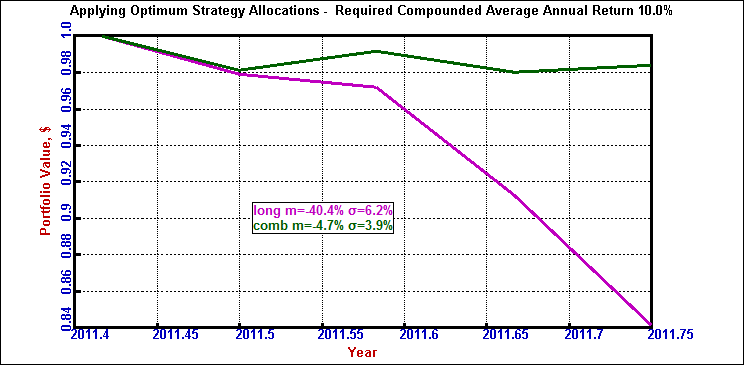
During the months of this mostly fear-driven event, the MMPT portfolio lost at a rate of only 4.7% compounded annually (green line) while the classic MPT portfolio lost money at an annual rate of -40.4% (magenta line). Further, the MMPT portfolio was less volatile. It experienced a standard deviation of only 3.9% while the classic MPT investor experienced a standard deviation of 6.2%.
Figure 1. Comparison of results
(green = MMPT)
(magenta = MPT)
Summary
We have shown that an MMPT investor during the global debt crisis was able to hold onto almost all of his money while most other investors were getting hammered. The reason is that a considered and properly applied market timing approach injects an element of flexibility and responsiveness to a portfolio while still benefiting from historical experience. This is of tremendous value especially in today’s uncertain markets.
Every day the news concerning the uncertainty of the global economy is increasing volatility across most of the traditional asset classes, and it’s for this reason that market timing approaches should be given their proper due. I believe we have shown once again with this case study that the MMPT approach combines the best of Modern Portfolio Theory with the desirability of a viable market timing strategy
For further information on how you can save your portfolio from the ravages of market crashes please visit our website.
*Previous articles on Surviving Market Crashes:
Part I: “Surviving Market Crashes”, August 23, 2011
Part II: “Surviving Market Crashes, Part 2: The dot-com bust”, September 29, 2011
Part III: “Surviving Market Crashes, Part 3: The subprime mortgage crisis”, November 19, 2011